首页注释:本案例讲述钢筋混凝土梁疲劳后剩余承载力试验。本案例涉及到的内容主要有钢筋混凝土梁疲劳剩余承载力试验设计、实验现象与实验结果分析、剩余承载力退化研究。作者:刘芳平,桥梁与隧道工程专业,工学博士,副教授,硕士生导师,主要从事桥梁结构监测与检测、加固与评定、结构性能退化等方面的研究;工作单位:重庆三峡学院。
摘要:对于长期经受循环荷载作用的桥梁,会在结构内部造成疲劳损伤累积,且损伤累积会随着荷载循环次数的增加而不断增长,造成结构承载能力的持续降低,严重威胁桥梁安全。本案例是针对钢筋混凝土梁的疲劳问题,结合理论推导使学生对钢筋混凝土梁疲劳后剩余承载力有深入的了解,熟悉掌握钢筋混凝土梁的疲劳问题试验分析过程,组织学生进行其它类似案例的练习,为学生今后进行科研提供理论支撑和一定经验。
关键词:钢筋混凝土梁;循环荷载;疲劳损伤;剩余承载力;
引言:桥梁是公路交通系统的“咽喉”,在国家交通运输体系中占据重要位置。钢筋混凝土梁是我国公路桥梁中最主要的形式,比重达85%以上,其设计,施工,运营等一直受到广大从业人员关注。钢筋混凝土桥梁服役期间随使用动荷载、随机自然荷载等循环荷载作用,对结构疲劳耐久性造成了无法忽视的影响。随汽车数量、载重量增加,结构负担加重,在受循环荷载损伤过程中,随循环次数增加,损伤不断积累,承载能力持续下降,破坏进程加速,最终导致结构疲劳失效破坏,严重威胁桥梁安全。
背景介绍:结合本人重庆市科委自然科学基金项目《疲劳荷载下RC梁基于刚度退化的承载力退化规律计算模型及实验研究》,本案例进行了钢筋混凝土梁的疲劳试验设计、实验现象与实验结果分析、结合理论分析进行了剩余承载力退化研究。探索了疲劳荷载作用下钢筋混凝土梁承载力退化的规律。
内容:
一、试验设计
(一)试验概况
本文共对5片钢筋混凝土梁进行疲劳试验研究,主要测试以下量的发展变化情况:①随疲劳循环次数增加,疲劳应变(包括:疲劳残余应变和疲劳总应变)的发展变化情况;②随疲劳循环次数增加钢筋混凝土梁裂缝以及梁挠度变化情况。
5片试验梁中,1片梁做静载试验,其余4片梁做等幅疲劳试验。试验在重庆交通大学结构试验室进行,静载破坏试验与等幅疲劳试验均在MTS疲劳试验机(加载吨位为250KN)上完成。
(二)试验工况
在实验室内共浇筑同一批次矩形截面梁5根,编号为JL-1~JL-5,其中JL-1进行静载试验来获取疲劳试验所需的极限荷载;JL-2~JL-4梁进行不同荷载水平下疲劳试验,获取整个寿命周期内的各种信息;JL-5梁在JL-4梁获取疲劳寿命基础上在加载至约0.8倍疲劳寿命时进行静载破坏试验,以此获取剩余承载力信息。
(三)试验加载方法
1.静载试验
预载的控制值设定为30KN,分三级进加载,并分2-3次完成卸载。预载完成后进行静载的破坏试验,采取分级加载的方式来进行,初始荷载增量定为20kN,在接近试验梁的屈服荷载后,减小荷载等级为10kN;同时对裂缝出现的位置形态进行观察与记录,在梁将要破坏时,进一步减小荷载等级至5KN,详细记录梁破坏时的过程和形态。最终加载至梁破坏,得到钢筋混凝土梁的开裂荷载以及极限承载力。静载试验的主要目的有两个:一是确定疲劳试验所需的静力极限荷载以及开裂荷载;二是判定试验梁配筋是否合适。
2.疲劳试验
在正式进行疲劳实验前首先同样对试件进行3次预载,以检查数据采集系统是否正常工作,试验加载控制是否安全可靠。两者都正常后才开始试验。试验采用荷载幅度进行控制,故在等幅疲劳试验时,首先将荷载分级加载至
 ,设定荷载幅为
,设定荷载幅为
 ,输入荷载频率与下一次疲劳循环加载的目标次数,为防止当有意外发生时加载系统自然停止,设定好位移与力的保护限值,之后在进行荷载试验。在荷载循环至1次、1000 次、1 万次、2 万次、5 万次、10 万次、20万次以后每隔20万次时停止疲劳试验,将荷载
,输入荷载频率与下一次疲劳循环加载的目标次数,为防止当有意外发生时加载系统自然停止,设定好位移与力的保护限值,之后在进行荷载试验。在荷载循环至1次、1000 次、1 万次、2 万次、5 万次、10 万次、20万次以后每隔20万次时停止疲劳试验,将荷载
 卸载至 0,然后对各采集装置进行调零处理,将百分表放置好,使指针与粘贴在梁体侧面的L型扣件充分接触。然后采集下0KN 状态下,结构的位移及应变信息。然后每隔20KN分级加载至疲劳荷载上限
卸载至 0,然后对各采集装置进行调零处理,将百分表放置好,使指针与粘贴在梁体侧面的L型扣件充分接触。然后采集下0KN 状态下,结构的位移及应变信息。然后每隔20KN分级加载至疲劳荷载上限
 ,测得各个时刻的位移及应变信息,与此同时对每次疲劳荷载上限
,测得各个时刻的位移及应变信息,与此同时对每次疲劳荷载上限
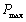 时的裂缝长度及宽度做好记录,记录完成后,将百分表移开,将荷载逐渐加载至
时的裂缝长度及宽度做好记录,记录完成后,将百分表移开,将荷载逐渐加载至
 ,继续进行疲劳试验。试验最初始从0加至
,继续进行疲劳试验。试验最初始从0加至
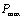 时的状态作为第1次疲劳循环加载。本文试验疲劳加载的频率为5Hz。
时的状态作为第1次疲劳循环加载。本文试验疲劳加载的频率为5Hz。
(四)测试内容及数据采集
1.测试内容
本试验中需要获取的数据有受拉区钢筋应变、受压区混凝土应变、跨中挠度、裂缝宽度及长度、支座位移、疲劳寿命N。
2.测点布置
实验梁钢筋应变、混凝土应变、挠度各测点布置见图1所示。

(a)测点立面布置
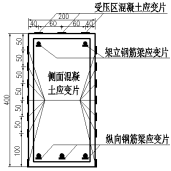
(b)测点横断面布置
测点布置图1
二、试验现象与结果
(一)试验现象描述
1.静载试验;
JL-1梁为静载实验梁,目的主要测试钢筋混凝土实验梁的开裂荷载与极限荷载。从梁的破坏过程可以看出,当荷载达到开裂荷载时,首先在梁的跨中纯弯曲段出现7~8条裂缝,基本呈对称分布,都沿着竖直分布,裂缝高度较小,裂缝最大宽约为0.08mm。随着实验荷载不断增加,试验梁的裂缝数目不断增多,但是仍然大致沿梁中心呈对称分布,原有裂缝宽度明显的在慢慢变宽。随着荷载等级的进一步提高,会听到“砰”的响声,这时纵向受拉钢筋开始屈服,此时钢筋混凝土实验梁跨中和纯弯曲段出现大量裂缝(约40条),少许裂缝沿着梁高延伸至梁顶面受压区,裂缝宽度值在0.1mm~0.2 mm间。经计算,本钢筋混凝土实验梁的配筋率为
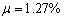 ,最小与最大配筋率为
,最小与最大配筋率为
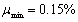 ,
,
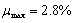 ,
,
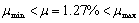 ,纵向受拉钢筋满足适筋的要求,试验情况和理论计算比较吻合。最终测得开裂荷载为40KN,极限承载力为220KN。钢筋混凝土静载试验梁加载情况如图2;静载实验梁裂缝部分情况如图3;跨中主裂缝与梁底裂缝如图4。
,纵向受拉钢筋满足适筋的要求,试验情况和理论计算比较吻合。最终测得开裂荷载为40KN,极限承载力为220KN。钢筋混凝土静载试验梁加载情况如图2;静载实验梁裂缝部分情况如图3;跨中主裂缝与梁底裂缝如图4。

图2 静载试验加载情况

图3 静载试验梁裂缝分布情况

(a) 跨中主裂缝

(b) 跨中梁底裂缝
图4 静载试验梁局部裂缝情况
2.疲劳试验
对JL-2~JL-4梁进行疲劳全寿命的观测,3片梁的破坏过程非常类似。在疲劳试验之前,首先按照20KN荷载步进行一次静载,加载至疲劳上限,在这个过程中同步进行应变、挠度等信息数据的采集,将此作为疲劳试验循环1次的试验结果。在疲劳第1次循环时,JL-2~JL-4梁的荷载取值都比较大,上限分别为132KN、154KN、176KN,荷载值都超过实验梁的开裂荷载,所以在纯弯曲段和弯剪区都会出现多条裂缝;其中JL-2梁出现12条,JL-3梁出现16条,JL-4梁出现21条,裂缝都沿跨中对称分布,纯弯曲段裂缝基本为竖直,弯剪区大概为45°方向,裂缝间距大概在10~20cm,裂缝长度不超过梁高度的一半,宽度不超过0.1mm。卸载以后很多裂缝自动闭合。
疲劳循环次数不断增大,当达到1000次,10000次,20000次,50000次,通过外观检查发现,在这期间3片梁裂缝的发展都比较迅速。疲劳荷载循环到1000次时,JL-2梁裂缝出现5条,JL-3梁裂缝出现5条,JL-4梁裂缝出现7条;疲劳荷载循环到1万次时,2万次时,5万次时,JL-2~JL-4梁裂缝出现都在3~7条之间,1万次以后整个梁开始出现斜裂缝,并向分配梁两个加载点方向延伸,但是很多条裂缝的宽度都在0.1mm以下,有个别裂缝最大值达到了0.2mm。
超过20万次后新的裂缝偶尔有1~2条,原来裂缝都有延伸,逐渐变宽。底部混凝土轻微剥落,两个加载点也有混凝土轻微剥落。随着疲劳循环次数的增加,裂缝的发展变得比较缓慢,裂缝长度、裂缝宽度以及数量并没有明显的增长、增宽与增多,说明钢筋混凝土试验梁退化比较缓慢。
将位移保护限值加大,在进行疲劳试验,大约疲劳循环几百次后梁因钢筋的屈服、裂缝短时间内发展变的很大,梁的挠度变形很大,最终在不加大荷载对试验梁进行静载时其完全破坏。
JL-2~JL-4梁的破坏方式相类似,裂缝的产生的条数略有不同,但是裂缝分布的形态基本上都一致,疲劳破坏的特征如图5所示(以JL-2为例)。

(a)试验梁裂缝分布

(b)跨中主裂缝

(c)分配梁下混凝土局部压碎

(d)跨中裂缝已经贯通、受压区混凝土压碎

(c)纯弯曲段裂缝分布

(d)弯剪段裂缝分布
图5试验梁疲劳特征
JL-2~JL-5梁的试验结果如表1所示。
表1 JL-2~JL-5梁试验结果
梁编号
|
疲劳荷载
|
破坏情况
|
疲劳寿命
|
JL-2
|


|
梁破坏时,全梁发现裂缝42条;竖向裂缝延伸至受压区顶部;受压区混凝土被压碎;主裂缝最大宽度1.7mm。
|
168万次
|
JL-3
|

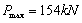
|
梁破坏时,全梁发现裂缝46条;竖向裂缝延伸至受压区顶部;受压区混凝土被压碎;主裂缝最大宽度1.9mm。
|
126万次
|
JL-4
|
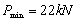
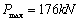
|
梁破坏时,全梁发现裂缝37条;竖向裂缝延伸至受压区顶部;受压区混凝土被压碎;主裂缝最大宽度1.9mm。
|
64万次
|
JL-5
|
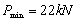

|
试验加载50万次以后进行静载破坏,测得破时荷载为
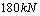
|
(二)试验结果
1.挠度
试验结果显示,随着疲劳循环次数的不断增加,当进行到各特定循环次数下,荷载作用在疲劳荷载上限时梁跨中的挠度不断增大,并且呈现出明显的三阶段发展趋势:疲劳过程中挠度的变化和静载过程中有相似的规律。表2为各个梁在不同的循环次数下当荷载作用在疲劳上限
 时的挠度。图6~12为不同循环次数时钢筋混凝土实验梁跨中挠度与荷载的关系曲线。
时的挠度。图6~12为不同循环次数时钢筋混凝土实验梁跨中挠度与荷载的关系曲线。
从图6~7可以看出,初次加载以及疲劳加载1000次时,各个梁跨中挠度与荷载的增长基本上呈现线性变化规律,荷载幅值与疲劳的影响不明显。从图8~12可以看出,三个梁的起点都向上进行了移动,说明残余挠度增加比较迅速,从挠度也间接说明开始疲劳损伤积累比较快,三个梁的挠度数值曲线慢慢开始分散,且在同等荷载下荷载水平较大的梁挠度较大,说明实验梁的荷载水平对梁的影响随疲劳循环次数的增加变的越来越明显。
表2 各循环次数下
 作用时跨中挠度(mm)
作用时跨中挠度(mm)
梁编号
|
JL-2(
 ) )
|
循环次数
|
1
|
1000
|
1万
|
2万
|
5万
|
10万
|
最大挠度
|
5.12
|
5.82
|
6.24
|
6.68
|
7.32
|
7.88
|
循环次数
|
20万
|
40万
|
60万
|
80万
|
100万
|
120万
|
最大挠度
|
8.46
|
9.02
|
9.65
|
10.12
|
10.56
|
11.03
|
循环次数
|
140万
|
160万
|
168万
|
|
|
|
最大挠度
|
11.88
|
13.24
|
13.74
|
|
|
|
|
JL-3(
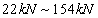 ) )
|
循环次数
|
1
|
1000
|
1万
|
2万
|
5万
|
10万
|
最大挠度
|
6.18
|
6.86
|
7.45
|
8.13
|
9.02
|
9.84
|
循环次数
|
20万
|
40万
|
60万
|
80万
|
100万
|
120万
|
最大挠度
|
10.33
|
10.98
|
11.54
|
12.00
|
12.78
|
13.20
|
循环次数
|
126万
|
|
|
|
|
|
最大挠度
|
13.36
|
|
|
|
|
|
|
JL-5(
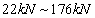 ) )
|
循环次数
|
1
|
1000
|
1万
|
2万
|
5万
|
10万
|
最大挠度
|
7.10
|
7.88
|
8.45
|
9.04
|
10.45
|
10.92
|
循环次数
|
20万
|
40万
|
60万
|
62万
|
|
|
最大挠度
|
11.58
|
12.24
|
13.82
|
14.88
|
|
|
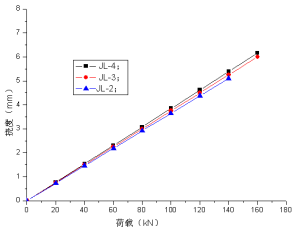
图6 循环荷载作用1次后静力加载荷载-挠度曲线
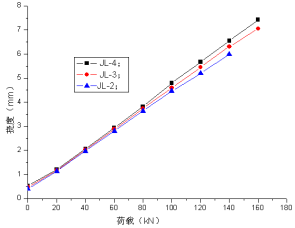
图7 循环荷载作用1000次后静力加载荷载-挠度曲线
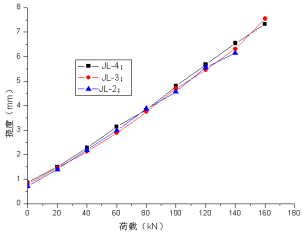
图8循环荷载作用1万次后静力加载荷载-挠度曲线

图9循环荷载作用2万次后静力加载荷载-挠度曲线
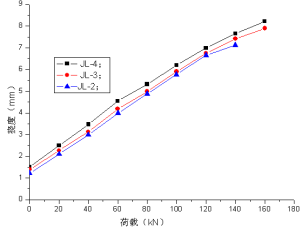
图10循环荷载作用5万次后静力加载荷载-挠度曲线

图11 循环荷载作用10万次后静力加载荷载-挠度曲线
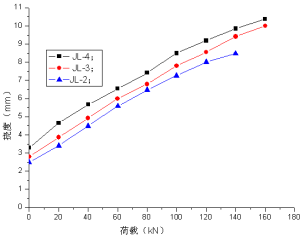
图12 循环荷载作用20万次后静力加载荷载-挠度曲线
2.混凝土应变结果
受压区混凝土应变会随着疲劳循环次数的增大而加大。在梁体疲劳初始阶段,疲劳加载次数较少,各梁的应变增加较快,超过2万次以后应变的变化慢慢趋向于稳定,临近疲劳破坏时,其应变又开始迅速扩展。应变的变化表明,钢筋混凝土梁的损伤也大致经历了这三个阶段,另外,钢筋混凝土梁疲劳前的损伤以及疲劳循环过程对混凝土应变的增大产生一定的影响,不同梁各不相同。JL-2~JL-4梁各循环次数后混凝土受压区荷载-应变曲线如图13~15所示。
图13~15结果表明,随着疲劳循环次数的增加,空载时受压区的混凝土应变不断增加;荷载作用下也一样,相同循环次数,3片梁总的残余应变累积也不同,总体呈现出应力水平越大,残余应变的累积越大;从3片梁的应变数据看出,随着荷载上限从
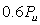 到
到
 再到
再到
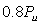 的过程中,各个梁混凝土受压区的应变增长基本上呈现线性变化。受压区混凝土应变的这一规律从一定程度上也反映了钢筋混凝土梁正截面抗弯刚度退化情况。
的过程中,各个梁混凝土受压区的应变增长基本上呈现线性变化。受压区混凝土应变的这一规律从一定程度上也反映了钢筋混凝土梁正截面抗弯刚度退化情况。
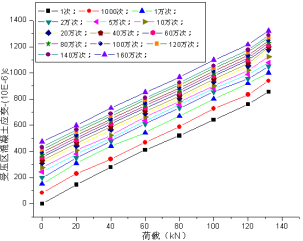
图13JL-2梁各循环次数后混凝土受压区荷载-应变曲线

图14 JL-3梁各循环次数后混凝土受压区荷载-应变曲线

图15 JL-4梁各循环次数后混凝土受压区荷载-应变曲线
注:图14~16中数据为受压区混凝土应变的平均值。
3.受拉钢筋应变结果
在循环荷载作用下,受拉区钢筋的应变在初期增长的比较快,变化比较明显,随着疲劳循环次数的不断增大,钢筋的应变增量有所下降,当疲劳循环次数进行到超过5万次时,受拉钢筋的应变进入了一个相对稳定增长阶段,临近疲劳破坏时,钢筋应变又开始迅速扩展。钢筋应变的变化和混凝土应变的变化有相似的三阶段变化规律。在第一次加载以后,受拉钢筋将产生疲劳塑性应变,随循环加载次数增大,总塑性应变一直在不断增加;从疲劳的过程来看,从疲劳1次→1000次→1万次→2万次→5万次的过程中疲劳残余应变增加的比较快,超过5万次以后疲劳残余应变增加的比较缓慢。JL-2~JL-4梁各循环次数后钢筋荷载-应变曲线如图16~18所示。
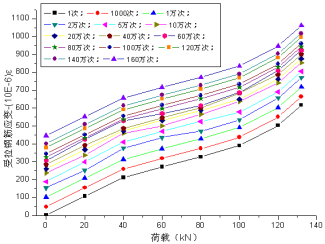
图16 JL-2梁受拉钢筋荷载-应变曲线

图17 JL-3梁受拉钢筋荷载-应变曲线
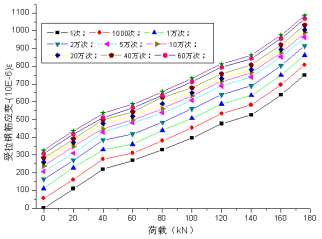
图18 JL-4梁受拉钢筋荷载-应变曲线
三、梁的疲劳剩余承载力研究
(一)分析理论
1.疲劳荷载作用下梁的刚度计算
疲劳刚度的定义
疲劳荷载作用于钢筋混凝土梁时,因材料性能衰减、梁的变形逐步增大、刚度慢慢减小,并且这种变化随着疲劳循环次数的增加呈现单调增大或减小。所以,研究梁的疲劳刚度,最关键其退化规律。
假定钢筋混凝土梁受到疲劳荷载时结构的初始刚度为
 (可取
(可取
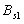 ),破坏时的刚度为
),破坏时的刚度为
 ,那么整个过程中刚度总共损失了
,那么整个过程中刚度总共损失了
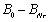 ,如果梁的刚度按照与疲劳寿命比有关的函数
,如果梁的刚度按照与疲劳寿命比有关的函数
 发生退化,则疲劳加载
发生退化,则疲劳加载
 次时梁刚度
次时梁刚度
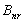 表达式为:
表达式为:
 (1)
(1)
将式子两边同时除以
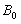 ,即:
,即:
 (2)
(2)
式(1)~(2)中:
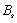 代表构件疲劳开始时候刚度,可取静载短期刚度;
代表构件疲劳开始时候刚度,可取静载短期刚度;
 为构件经过
为构件经过
 次疲劳荷载后的退化刚度;
次疲劳荷载后的退化刚度;
 代表疲劳破坏时退化刚度;
代表疲劳破坏时退化刚度;
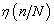 代表刚度退化函数;
代表刚度退化函数;
表达式(1)或表达(2)即为钢筋混凝土梁受到疲劳荷载作用时的刚度计算公式,其中初始刚度
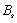 可基于试验通过测量挠度进行反算得到或基于有效惯性矩理论的方法进行计算。破坏刚度
可基于试验通过测量挠度进行反算得到或基于有效惯性矩理论的方法进行计算。破坏刚度
 可基于试验通过测量挠度进行反算得到。所以,要得到梁的疲劳刚度,关键在于确定刚度的退化函数
可基于试验通过测量挠度进行反算得到。所以,要得到梁的疲劳刚度,关键在于确定刚度的退化函数
 。
。
2.疲劳刚度退化函数的确定
(1)退化函数的选择
按照目前研究成果,钢筋混凝土梁疲劳刚度退化函数
 必需要满足以下所示的边界条件(a)、边界条件(b)而且还要具有变化规律(c) [10-11]:
必需要满足以下所示的边界条件(a)、边界条件(b)而且还要具有变化规律(c) [10-11]:
(a)在受到疲劳荷载之前钢筋混凝土梁未损伤,也就是说当
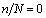 时,梁的刚度退化函数
时,梁的刚度退化函数
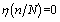 ,这时梁的刚度即为初始刚度
,这时梁的刚度即为初始刚度
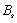 ;
;
(b)钢筋混凝土梁在破坏时损伤最大,也就是说当
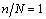 时,梁的刚度退化函数
时,梁的刚度退化函数
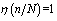 ,这时梁的刚度即为破坏刚度
,这时梁的刚度即为破坏刚度
 ;
;
(c)钢筋混凝土梁的刚度在疲劳初期、构件接近破坏阶段下降较快,而中间较长时间基本呈线性退化,呈现为S型退化规律;
符合条件(a)和(b)的函数构造较容易,但满足条件(c)的函数选取难度较大。经过不断尝试,选择了满足上面三点要求的函数如下:
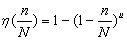 (3)
(3)
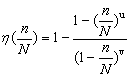 (4)
(4)
函数表达式(4)为廉伟在研究复合材料刚度时采用的刚度退化函数,也得到了不错好的效果。
将函数表达式(3)与函数表达式(4)代入(2)式后,可得到下面两式:
 (5)
(5)
 (6)
(6)
由上两式可知,要研究钢筋混凝土梁的疲劳刚度退化情况,关键在于确定选取的退化函数参数值。
(2)退化函数参数的确定
使用实验数据对刚度退化函(5)与(6)采用origin软件进行数据拟合。
3.基于刚度退化的承载力退化规律计算模型
(1)基于刚度退化的疲劳损伤
结构的刚度退化外在反映了梁的损伤情况,而疲劳过程中的刚度可以通过测试挠度再经过反算得到,简单且易行。为此,本文将钢筋混凝土梁疲劳刚度作为判定梁损伤的指标,在上述提出的疲劳刚度计算表达式基础之上,建立了疲劳刚度与梁结构损伤之间的关系式。
参考廉伟在研究复合材料刚度与结构损伤的关系,可将钢筋混凝土梁疲劳损伤的程度用以下规律表征:
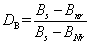 (7)
(7)
式中:
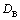 为利用刚度定义的损伤变量,
为利用刚度定义的损伤变量,
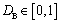 ;
;
(2)基于承载力退化的疲劳损伤
和刚度情况相似,结构的承载力退化也外在反映了梁的损伤情况,即可认为梁的承载力退化是结构损伤的另一种表现方式。参考FONG的损伤研究成果,得到三点假定:
(a)在疲劳加载过程中材料产生损伤,致使结构刚度和承载力两者都发生了下降;
(b)随疲劳循环次数增大,损伤积累逐渐增加,此过程不可逆,那么结构刚度和承载力一直单调下降;
(c)疲劳同一时刻,内在损伤相同,其损伤值应该唯一,只是结构刚度与承载力这两个外在表现形式不同而已,所以,结构刚度和结构承载力必存在一确定关系。
基于以上三点假定,参照用刚度定义的疲劳损伤,可将基于承载力的疲劳损伤定义如下:
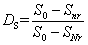 (8)
(8)
式中:
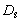 为利用承载力定义的损伤变量,
为利用承载力定义的损伤变量,
 ;
;
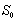 为构件的初始承载力;
为构件的初始承载力;
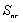 为经过
为经过
 次加载后的承载力;
次加载后的承载力;
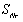 为构件破坏时,即
为构件破坏时,即
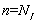 时的承载力;
时的承载力;
由疲劳承载力定义的损伤也可表述为疲劳寿命比的函数,设其为
 ,即:
,即:
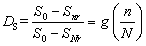 (9)
(9)
将式(9)进行正则化,变成(10)的形式,如下所示:
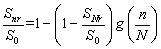 (10)
(10)
分析发现,与刚度退化函数同样,承载力退化函数
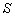 满足边界条件(a)、(b):
满足边界条件(a)、(b):
(a)构件在受到疲劳荷载前未损伤,即,
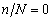 时,函数
时,函数
 ,此时的承载力为初始承载力,用
,此时的承载力为初始承载力,用
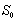 表示,通过静载试验、数值计算或理论分析等方式获得;
表示,通过静载试验、数值计算或理论分析等方式获得;
(b)构件破坏时损伤最大,即
 时,函数
时,函数
 ,承载力退化为
,承载力退化为
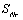 ,计算时可取构件破坏的试验加载最大值,即
,计算时可取构件破坏的试验加载最大值,即
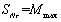 ;
;
(3)基于刚度退化的承载力退化模型
对比发现,由上述刚度定义的损伤
 与承载力定义的损伤
与承载力定义的损伤
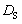 有如下3点共同特性:
有如下3点共同特性:
(a)刚度定义的损伤
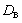 与承载力定义的损伤
与承载力定义的损伤
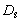 范围值都为
范围值都为
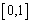 ;
;
(b)刚度定义的损伤
 与承载力定义的损伤
与承载力定义的损伤
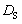 疲劳初始值都为0,破坏时值都为1;
疲劳初始值都为0,破坏时值都为1;
(c)刚度定义的损伤
 与承载力定义的损伤
与承载力定义的损伤
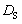 在
在
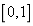 上都是单调增函数;
上都是单调增函数;
根据第三条特性,可将这两个损伤之间的关系做如下定义:
 (11)
(11)
将
 的表达式(7)与
的表达式(7)与
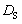 的表达式(9)带入(11)得到::
的表达式(9)带入(11)得到::
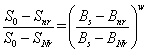 (12)
(12)
将(12)式进行处理即为:
 (13)
(13)
进行简单变换,变成如下所示:
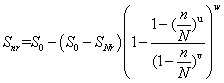 (14)
(14)
或者:
 (15)
(15)
式(14)或(15)即为本文建立的钢筋混凝土梁基于疲劳刚度退化的承载力退化规律计算模型。运用该模型,可依据刚度退化规律得到钢筋混凝土梁的承载力退化程度。
(二)疲劳刚度退化研究
本部分利用疲劳试验中JL-2~JL-4梁测得的挠度试验数据,结合静载作用下钢筋混凝土简支梁根据挠度得到的刚度表达式,计算得到不同疲劳荷载循环次数下的疲劳刚度,再通过非线性拟合的方法对本文提出的刚度退化函数的参数进行了确定,最终得到了实验梁在疲劳荷载作用下的刚度退化规律。
1.由挠度反算刚度
首先,在用刚度表达式进行挠度计算时,
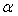 为挠度相关系数,与支撑条件与支撑形式等有关,考虑本文加载的试验方案,取
为挠度相关系数,与支撑条件与支撑形式等有关,考虑本文加载的试验方案,取
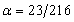 。试验梁初始刚度由第一次疲劳加载的挠度通过反算得到。钢筋混凝土梁经过
。试验梁初始刚度由第一次疲劳加载的挠度通过反算得到。钢筋混凝土梁经过
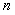 次疲劳荷载以后,刚度
次疲劳荷载以后,刚度
 (
(
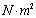 )可由下式进行计算:
)可由下式进行计算:
 (16)
(16)
式子(5.7)中,
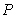 为与挠度
为与挠度
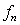 相对应的荷载,在此,取
相对应的荷载,在此,取
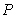 为疲劳上限荷载,
为疲劳上限荷载,
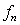 为每次加载到疲劳上限时的挠度。
为每次加载到疲劳上限时的挠度。
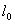 为梁的计算跨径。
为梁的计算跨径。
由试验测得的挠度表3按照式(16)计算得到的JL-2~JL-4梁的疲劳刚度数值见表4
表3试验刚度结果(刚度单位:
 )
)
JL-2梁
|
循环次数
|
1
|
1000
|
1万
|
2万
|
5万
|
10万
|
刚度
|
9.874
|
8.687
|
8.102
|
7.568
|
6.907
|
6.416
|
循环次数
|
20万
|
40万
|
60万
|
80万
|
100万
|
120万
|
刚度
|
5.976
|
5.605
|
5.239
|
4.996
|
4.788
|
4.483
|
循环次数
|
140万
|
160万
|
168万
|
|
|
|
刚度
|
4.256
|
3.818
|
3.697
|
|
|
|
JL-3梁
|
循环次数
|
1
|
1000
|
1万
|
2万
|
5万
|
10万
|
刚度
|
9.544
|
8.598
|
7.917
|
7.255
|
6.539
|
5.994
|
循环次数
|
20万
|
40万
|
60万
|
80万
|
100万
|
120万
|
刚度
|
5.710
|
5.372
|
5.111
|
4.915
|
4.615
|
4.068
|
循环次数
|
126万
|
|
|
|
|
|
刚度
|
3.615
|
|
|
|
|
|
JL-3梁
|
循环次数
|
1
|
1000
|
1万
|
2万
|
5万
|
10万
|
刚度
|
9.494
|
8.598
|
7.917
|
7.457
|
6.451
|
6.408
|
循环次数
|
20万
|
40万
|
60万
|
62万
|
|
|
刚度
|
5.974
|
5.507
|
5.061
|
4.463
|
|
|
在进行数据拟合之前,为了方便计算,将表4中的刚度进行无量纲化,拟合得到曲线如图19~图21。拟合得到的刚度退化函数参数如表4。
表4 所拟合的刚度退化函数参数
JL-2梁
|
拟合参数
|
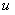
|
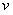
|
拟合精度
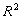
|
0.2171
|
0.4914
|
0.9840
|
JL-3梁
|
拟合参数
|
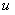
0.2247
|
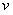
0.7044
|
拟合精度
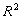
0.9880
|
JL-4梁
|
拟合参数
|
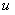
|
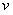
|
拟合精度
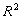
|
0.2362
|
0.6123
|
0.9753
|

图19 JL-2梁刚度退化的试验曲线与拟合曲线

图20 JL-3梁刚度退化的试验曲线与拟合曲线

图21 JL-4梁刚度退化的试验曲线与拟合曲线
将拟合得到的参数
 带入到刚度退化函数中,本实验中JL-2~JL-4梁,刚度退化函数将变为:
带入到刚度退化函数中,本实验中JL-2~JL-4梁,刚度退化函数将变为:
JL-2:
 (17)
(17)
JL-3:
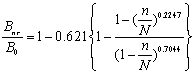 (18)
(18)
JL-4:
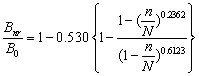 (19)
(19)
从拟合过程发现,参数
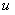 随着荷载水平的加大而稍微有所变大,通过和第四章实例进行比较,发现
随着荷载水平的加大而稍微有所变大,通过和第四章实例进行比较,发现
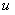 值越小的时候刚度退化曲线初始段的退化量越小、初始退化的速率越快。参数
值越小的时候刚度退化曲线初始段的退化量越小、初始退化的速率越快。参数
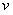 随着荷载水平的提高在不断增大,相比参数
随着荷载水平的提高在不断增大,相比参数
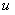 增加的较快,从图中可以看出临近破坏时的刚度退化速率加快。所以,初始退化速率在总体相差不大的情况下,JL-2梁相对较大,JL-4梁相对较小;临近破坏时随荷载水平加大,刚度下降的越快。
增加的较快,从图中可以看出临近破坏时的刚度退化速率加快。所以,初始退化速率在总体相差不大的情况下,JL-2梁相对较大,JL-4梁相对较小;临近破坏时随荷载水平加大,刚度下降的越快。
(三)疲劳承载力退化预测
为了研究本试验JL-2~JL-4梁在疲劳过程中承载力的退化情况,本文应用提出的基于刚度退化的承载力退化模型对试验梁承载力退化规律进行了比较分析。
1.关联参数
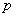 的求解
的求解
利用本文建立的绝对承载力退化模型式或者相对承载力退化模型对承载力进行分析的时候,首先要计算出模型中关联参数
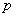 。在此,首先利用计算参数
。在此,首先利用计算参数
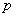 。中
。中
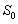 、
、
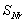 、
、
 分别为疲劳开始的承载力、实验梁破坏承载力,以及疲劳循环
分别为疲劳开始的承载力、实验梁破坏承载力,以及疲劳循环
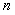 次后的承载力,在此可以取相对应的三个荷载,分别为静载作用下得到的荷载220kN,疲劳破坏时可取为JL-5梁疲劳上限值176 kN,以及JL-5梁疲劳循环50万次后的荷载180kN。参数
次后的承载力,在此可以取相对应的三个荷载,分别为静载作用下得到的荷载220kN,疲劳破坏时可取为JL-5梁疲劳上限值176 kN,以及JL-5梁疲劳循环50万次后的荷载180kN。参数
 可以取为刚度退化函数当中数值。得到:
可以取为刚度退化函数当中数值。得到:
 (20)
(20)
最终计算得到关联参数
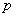 为0.6556。需要说明的是,本试验所取疲劳下限都为
为0.6556。需要说明的是,本试验所取疲劳下限都为
 ,JL-2~JL-4梁的疲劳上限
,JL-2~JL-4梁的疲劳上限
 ,
,
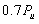 ,
,
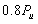 。参数
。参数
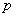 是在JL-4梁情况下联合JL-5梁实验得到的,因资金等主客观条件限制,没对JL-2~JL-3梁做对应的破坏试验来确定它们的关联参数
是在JL-4梁情况下联合JL-5梁实验得到的,因资金等主客观条件限制,没对JL-2~JL-3梁做对应的破坏试验来确定它们的关联参数
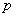 。因此,本文下面对JL-2~JL-3梁进行承载力退化分析时,仍然采用参数0.6556。
。因此,本文下面对JL-2~JL-3梁进行承载力退化分析时,仍然采用参数0.6556。
2.承载力退化规律
JL-2~JL-4梁的初始承载力根据初始荷载和试验中分配梁的布置位置为:
 ,同样破坏时各个梁的承载力为
,同样破坏时各个梁的承载力为
 ,
,
 ,
,
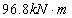 。将以上相关参数带入绝对承载力退化模型式中得到JL-2~JL-4梁的承载力退化方程式分别为:
。将以上相关参数带入绝对承载力退化模型式中得到JL-2~JL-4梁的承载力退化方程式分别为:
JL-2:
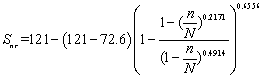 (21)
(21)
JL-3:
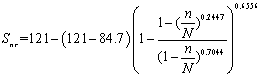 (22)
(22)
JL-4:
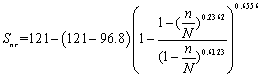 (23)
(23)
经过计算得到的JL-2~JL-4梁疲劳荷载作用下承载力退化规律如图22所示。
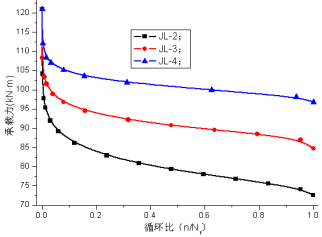
图22 JL-2~JL-4梁承载力退化曲线
因式中都为相对量值,将承载力数值都用相对应荷载代替,将以上相关参数带入相对承载力退化模型式中得到JL-2~JL-4梁的相对初始承载力退化方程式分别为:
JL-2:
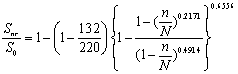 (24)
(24)
JL-3:
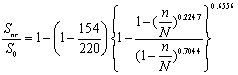 (25)
(25)
JL-4:
 (26)
(26)
经过计算得到的JL-2~JL-4梁疲劳荷载作用下承载力退化规律如图23~25所示。

图23 JL-2梁相对初始承载力的退化曲线
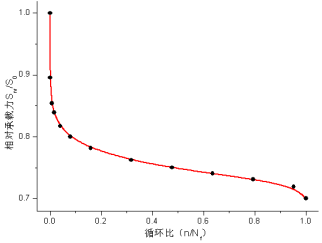
图24 JL-3梁相对初始承载力的退化曲线
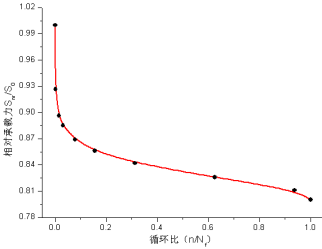
图25 JL-4梁相对初始承载力的退化曲线
钢筋混凝土梁疲剩余承载力实验研究案例
教学指导手册
教学目的与用途:
1.本案例适用于全日制土木水利工程类硕士专业结构工程方向研究生的方向选修课程《桥梁设计理论》。桥梁工程中,对于长期经受循环荷载作用的桥梁,会在结构内部造成疲劳损伤累积,且损伤累积会随着荷载循环次数的增加而不断增长,造成结构承载能力的持续降低,严重威胁桥梁安全。所以对钢筋混凝土梁疲劳后剩余承载力研究是必不可少的,对保证桥梁正常使用有着重要的意义。
2.通过此教学案例,使研究生掌握钢筋混凝土梁疲劳后剩余承载力试验研究内容、目的及过程、并结合钢筋混凝土梁的疲劳试验,将开裂荷载与极限荷载试验值与理论计算值进行了对比分析;将经过特定疲劳次数后的钢筋混凝土试验梁的剩余承载力与基于材料强度疲劳耗散的承载力计算结果进行了比较;结合试验对钢筋混凝土梁基于疲劳刚度退化的承载力退化模型进行了验证,探索疲劳荷载作用下钢筋混凝土梁承载力退化的规律。此外,此教学案例也可用于道路与桥梁工程相关本科专业的教学。
3.通过案例讲解使学生对钢筋混凝土梁疲劳后剩余承载力试验主要内容、目的、流程等有深入的了解,在此基础上通过组织学生进行其它类似案例的实践,为学生今后进行科研、工程建造提供理论支撑和实践经验。
教学内容:
1.涉及知识点
(1)钢筋混凝土梁的疲劳试验设计;
(2)钢筋混凝土梁的疲劳试验现象与实验结果分析;
(3)试验验证钢筋混凝土梁基于疲劳刚度退化的承载力退化模型。
2.理论依据及分析思路
(1)理论依据:
桥梁工程中,对于长期经受循环荷载作用的桥梁,会在结构内部造成疲劳损伤累积,且损伤累积会随着荷载循环次数的增加而不断增长,造成结构承载能力的持续降低,严重威胁桥梁安全。所以对钢筋混凝土梁疲劳后剩余承载力研究是必不可少的,对保证桥梁正常使用有着重要的意义。
(2)分析思路
本案例刚开始是简述试验设计包括(试验目的、试验方案、试验工况、试验装置与加载方法),然后分析试验现象与结果,再进行钢筋混凝土梁的疲劳承载力退化研究。
本案例结合自身特点,按照钢筋混凝土梁疲劳后剩余承载力试验来进行分析与讲解的。
建议课堂计划:
时间安排:根据教学需要,整个案例课的课堂时间控制在6学时,以便比较充分地了解案例所涉及的知识点,以下是根据课程时间进度安排的课堂学习计划。
课前计划:发放案例材料,提出课后思考题,请学生在课前完成阅读和初步思考。
课中计划:课堂前言,明确该案例主题(20分钟);案例讲述,案例总体介绍,引导学生分析和认真学习该案例的理论知识点,并提出思考题(120分钟);分组讨论(20分钟);小组发言(20分钟一个小组,4组);案例总结:包括案例中的关键知识点,以及如何运用理论知识去分析和解决实际问题(30分钟)。
课后计划:通过案例分析和总结,使学生掌握施工监控知识,然后布置相关作业,以论文或者报告形式写出案例分析,并对难点和易错点可以进一步研究。
参考文献:
1.唐先习.疲劳荷载作用下铰接板桥挠度试验.长安大学学报(自然科学版), 2014.
2.沈忠斌.疲劳荷载作用下钢筋混凝土受弯构件使用性能的试验研究.东南大学,1989.
3.朱晓东.重复荷载作用下钢筋混凝土梁正截面刚度的试验研究 东南大学,1989.
4.赵国藩.高等钢筋混凝土结构学.北京:中国电力出版社,1999
5.曾志斌.普通混凝土梁用钢筋的疲劳S-N曲线研究.土木工程学报, 1999
6.贡金鑫.随机反复荷载下钢筋混凝土受弯构件变形的计算分析.工业建筑,2002
7.查全璠.钢筋混凝土梁疲劳性能国内外研究综述.世界桥梁, 2004
8.潘华.钢筋混凝土受弯构件正截面疲劳性能数值模拟.东南大学学报, 2006.
9.王海超.腐蚀疲劳钢筋混凝土梁正截面应变分析.建筑结构学报, 2007
10.李星新.钢筋混凝土桥梁疲劳时变可靠度分析.中国铁道科学, 2009
11.蒋丽忠.钢筋混凝土空心梁疲劳性能试验研究.铁道科学与工程学报, 2010.
12.朱劲松.钢筋混凝土桥梁疲劳累积损伤失效过程简化分析方法.工程力学, 2012.
13.宋玉普.疲劳荷载作用下梁内不同类型钢筋破坏关系.哈尔滨工业大学学报, 2012.
14.朱红兵.钢筋混凝土空心板梁疲劳损伤试验研究.桥梁建设, 2013.
15.朱红兵.钢筋混凝土T梁疲劳性能试验研究.公路交通科技, 2013.
16.王新玲. HRBF500钢筋混凝土梁受弯疲劳性能理论研究.建筑结构, 2014.